Taganrog, Rostov-on-Don, Russian Federation
CSCSTI 06.81
CSCSTI 06.01
Russian Classification of Professions by Education 38.06.01
Russian Library and Bibliographic Classification 65
Russian Trade and Bibliographic Classification 7717
According to the theory of system analysis, the concept of the goal in a complex system can not be completely unambiguously defined. A complex system usually has a hierarchical structure. The overall objective of the system exists, but the challenge is to describe it and achieve implementation. To do this, the overall global goal is divided into sub-goals, clear at each level of the hierarchy. In addition, from the standpoint of system analysis, the goal at each level is not only a goal, but also a means to achieve the goal at a higher level. To describe the interaction of goals and means to achieve them, the so-called "goal tree"was proposed. For the correct construction of a tree of objectives is necessary to solve two questions [5]. The first is to consider all the many problems that arise when building a goal tree. The second is to attract experts to choose the best solution from a variety of possible alternative solutions. Developers in the secondary housing market are faced with the problem of choosing when to determine which housing mainly.
Method of analysis
Рынок жилья в г. Таганроге активно развивается. Многие девелоперы продолжают успешно работать на этом рынке, однако существуют некоторые трудности. Согласно [9] по состоянию на 06 ноября 2017, средняя цена за квадратный метр квартиры на вторичном рынке в городе Таганрог составляет 38 257 руб., за прошедшую неделю цена повысилась на 0.16% ( 61 руб.)
Средняя цена на квартиры в городе Таганрог — 1 984 046 руб.
Средние цены на квартиры Ростовская обл., г. Таганрог, изменение за неделю приведены в табл. 1.
Таблица 1
Средние цены на квартиры
|
Количество комнат |
Цена |
Рост цены |
|
1 комн. квартира. |
1 453 568 руб. |
(0.16%) |
|
2 комн. квартира. |
1 989 737 руб. |
(0.25%) |
|
3 комн. квартира. |
2 469 717 руб. |
(0.29%) |
|
4+ комн. квартира. |
3 187 250 руб. |
(0.92%) |
Средние цены за м2 и относительные цены Ростовская обл., г. Таганрог, изменение за неделю, приведены в табл.2.
Таблица 2
Средние цены за 1 м2 относительные цены
|
Количество комнат |
Цена |
Рост цены |
Относительно среднерыночной |
Относительно среднерыночной |
|
1 комн. квартира. |
39 747 руб. |
(0.12%) |
-45.40% |
- 18 044 руб. |
|
2 комн. квартира. |
38 243 руб. |
(0.15%) |
-43.17% |
- 16 510 руб. |
|
3 комн. квартира. |
36 798 руб. |
(0.21%) |
-44.46% |
- 16 361 руб. |
|
4+ комн. квартира. |
35 627 руб. |
(0.66%) |
-52.92% |
- 18 852 руб. |
На рис.1 приведен график изменения средней цены за последний месяц.
Рис.1 Изменение средней цены за 1м2
Из таблицы 2 можно увидеть, что несмотря на рост цен на вторичное жилье, цена 1 м2 квартир значительно отстает от среднерыночной. Кроме того, по данным [10] в октябре средняя площадь квартир в новостройках составила 49,3 кв. метра. До 2012 г. средняя площадь квартир была 64,6 кв. метра. За 4 года средний метраж квартир снизился более чем на 25%. Главной причиной уменьшения метража был не кризис, а растущая конкуренция. Привлечь покупателей стремились доступными ценами.
Это обстоятельство заставляет девелоперов, работающих на вторичном рынке, искать новые возможности для оживления рынка недвижимости. Для решения этой проблемы возможно воспользоваться мнениями и советами экспертов. Проанализировав все возможные варианты, эксперты пришли к выводу, что в сложившихся условиях на сегодняшний день для покупателей вторичного жилья самыми главными факторами являются наличие и близость транспортной инфраструктуры и состояние квартиры, т.е. наличие ремонта. Для девелоперов возникает вопрос, с каким жильем предпочтительно работать, операции с какими квартирами принесут наибольшую прибыль. Для решения данной задачи воспользуемся методом анализа иерархий.
Важным понятием системного анализа является система. Разделение системы на подсистемы элементы делается для того, чтобы лучше понять систему, которую анализируем. Структура показывает как элементы системы связаны друг с другом. Иерархическая структура используется для описания функции системы и целей системы.
В работе [4] разделяют методы моделирования систем на два больших класса:
- методы формального представления систем;
- методы, направленные на активизацию использования интуиции и опыта специалистов.
На сегодня методов, направленных на активизацию использования интуиции и опыта специалистов разработано достаточно много, они отличаются формой работы с экспертами и способами обработки экспертных оценок.
Иерархия есть определенный тип системы, основанный на предположении, что элементы системы могут группироваться в несвязанные множества. Элементы каждой группы находятся под влиянием элементов некоторой вполне определенной группы и, в свою очередь, оказывают влияние на элементы другой группы [6].
Иерархии являются основным способом, с помощью которого человек подразделяет реальность на кластеры и подкластеры [6].
Под согласованностью подразумевается то, что при наличии основного массива необработанных данных все другие данные логически могут быть получены из них [6].
Дерево целей начинается с формулирования основной цели, которая находится на самом высоком уровне. Далее эта цель разбивается на подцели, которые направлены на то, чтобы основная цель была выполнена. Эти подцели расположены на один уровень ниже. Далее подцели разбиваются на более мелкие, которые расположены еще на один уровень ниже и т.д. до тех пор, пока цели не станут неделимыми. Получаемое таким образом дерево направлено ветвями вниз.
Цели определяются после формулирования проблемы, которую нужно решить. Цель – это желаемый результат функционирования системы. Критерий – способ сравнения альтернатив [1]. Согласно правилам системного анализа, критерии формулируются после того, как заданы цели системы. Формирование критериев – очень сложная задача. Здесь активно применяются неформальные процедуры. Таким образом, выбор модели, выбор критерия – задачи принятия решения. Процедура принятия решения представляет собой действие над множеством альтернатив, в результате которого получается подмножество выбранных альтернатив.
Основные проблемы, возникающие при решении задач принятия решений, заключаются в том, что альтернативы могут отличаться одна от другой и выбор альтернативы – также задача принятия решения [1].
Сложности задач принятия решений обусловлена особенностями таких задач. Одной из таких особенностей является неопределенность, которая может появляться на всех этапах системного анализа.
Неопределенность, встречающуюся в задачах принятия решений, подразделяют на стохастическую и расплывчатую, дискретного типа и непрерывного.
Для описания дискретной неопределенности, когда имеется множество альтернатив X и множество исходов этих альтернатив Y , в качестве qij принимают оценку ситуации, когда в результате альтернативы xi получили исход yj. Результаты всех возможных альтернатив и исходов приводятся в виде таблицы 2 [1]:
Таблица 2
Возможные исходы альтернатив
|
X/Y |
y1 |
… |
yj |
|
x1 |
q11 |
… |
q1j |
|
… |
|
|
|
|
xi |
qi1 |
|
qij |
При одинаковых значениях в строках матрицы выбор без альтернативы, если же строки матрицы имеют разное значение, то возникает проблема выбора наилучшей альтернативы. Выбор модели представляет проблему принятия решения. Когда математический аппарат для выбора модели определить сразу не получается, считают, что возникла проблема, и необходимо определить область проблемы принятия решения [3]. Необходимо подобрать приемы и методы, позволяющие эту проблему решить.
Для рассматриваемого нами случая выбрали подход к отображению связи цели со средствами «сверху» [3,8], в виде дерева целей.
Метод анализа иерархий разработан Т. Саати в конце 1970-х гг. Метод использует парное сравнение для оценки своих компонент.
Метод парных сравнений – один из методов организации сложных экспертиз.
Согласно методике системного анализа [3, 4], на первом уровне ставится общая задача, это уровень цели. На втором уровне выбираются критерии, а на третьем происходит оценка альтернатив и выбор наилучшего решения. Пример наиболее простой иерархической модели приведен на рис. 2.
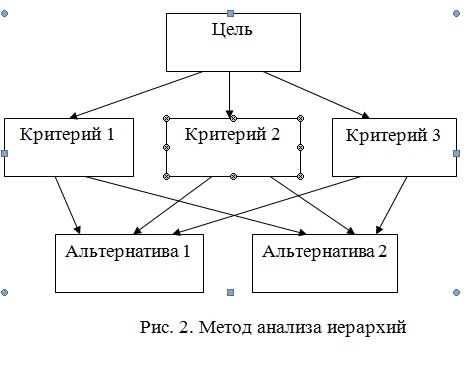
Между уровнями задаются матрицы. Матрица первого уровня задается для сравнения критериев по отношению к цели. Матрицы второго уровня задаются для оценки альтернатив относительно каждого из критериев. Число матриц второго уровня равно числу критериев. Числа для сравнения задаются в диапазоне от 1 до 9 согласно степени важности. Оценивают не более 7 + 2 составляющих на каждом уровне [6].
Рассмотрим более подробно применение метода парных сравнений на примере [6].
Предположим, девелопер имеет возможность работать с разными квартирами: однокомнатными G1, двухкомнатными G2, трехкомнатными G3. Требуется оценить их по двум критериям: наличие транспортной инфраструктуры и наличие ремонта в квартире. Критерий транспорт обозначим как T и критерий наличия ремонта обозначим как R. Для этого составим матрицу парных сравнений A. Матрица будет иметь размерность 2´2.
Эксперт считает, что наиболее предпочтительным критерием является ремонт. Согласно этому критерию, эксперт элементу (2,1) матрицы A задает значение 6, т.е. a21 = 6. Поэтому элемент (1,2) матрицы A имеет значение 1/6, т.е. a12 =1/6. Главная диагональ содержит единицы. Получим матрицу


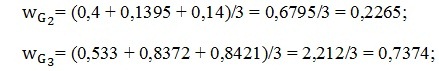
Матрица AТ не является согласованной, так как столбцы нормированной матрицы NТ не одинаковы.
Если матрица является несогласованной, вычисляется коэффициент согласованности для проверки того, можем ли мы воспользоваться результатами экспертного опроса или нет [6, 10].
Для этого в нормализованной матрице A¢ вычисляется среднее значение



Таблица 2
Экспертные оценки по заданным критериям
|
Критерии |
Квартиры |
||
|
G1 |
G2 |
G3 |
|
|
Транспорт |
0,071 |
0,227 |
0,7 |
|
Ремонт |
0,65 |
0,22 |
0,13 |
Как было вычислено ранее, веса критериев следующие:
wT=0,4; wR=0,6.
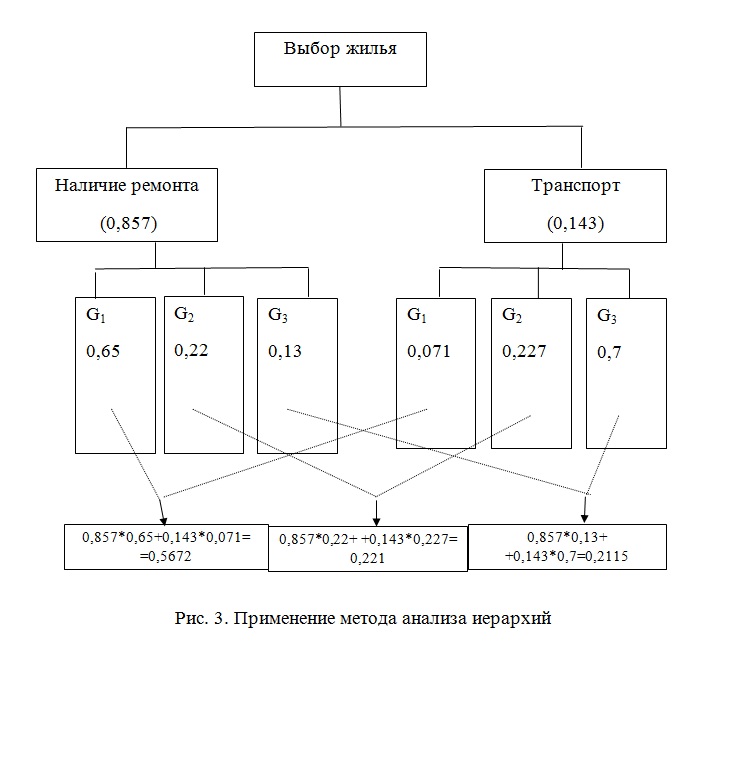
Метод анализа иерархий удобно представлять в виде графиков (рис. 3) [2, 7].
Выбор наилучшей альтернативы происходит следующим образом. Вычисляются комбинированные весовые коэффициенты для каждого варианта квартир.
Для однокомнатной квартиры G1 это будет
0,857*0,65+0,143*0,071 =0,5672.
Для двухкомнатной квартиры G2 это будет
0,857*0,22+ 0,143*0,227=0,221.
Для трехкомнатной квартиры G3 это будет
0,857*0,13+0,143*0,7=0,2115.
Наибольший вес получила однокомнатная квартира G1, поэтому рекомендуется работать именно с такими квартирами. Что касается двухкомнатных и трехкомнатных, то для этих квартир веса примерно одинаковы, и здесь особенных предпочтений нет.
Выводы. Метод анализа иерархий (МАИ) удовлетворяет требованиям, предъявляемым к научному обоснованию методов принятия решений [6]:
- Способы получения информации от эксперта соответствуют данным психологических исследований о возможностях человека переработать информацию.
- В МАИ имеется возможность проверки экспертной информации на непротиворечивость.
- Любые соотношения между вариантами решений в МАИ объяснимы на основе информации, полученной от экспертов.
- Математическая правомочность решающего правила в МАИ прозрачна и базируется на метода собственного значения и принципа иерархической композиции, имеющих четкое математическое обоснование.
Используя экспертные оценки, составили матрицы парных сравнений для выполнения расчетов. На примере убедились, что возможно решать задачу выбора правильного решения на рынке вторичного жилья с помощью метода анализа иерархий. Благодаря этому возможно сделать вывод о том, что возможно применение метода анализа иерархий для оценки недвижимости.
Заключение. Согласно теории принятия решений, для принятия решений важно выбрать способ связать цель со средствами ее достижения. Основные требования для достижения цели формулируются в виде критериев, дополнительные требования – в виде ограничений. Метод анализа иерархий, рассмотренный в данной работе, позволяет связать цель со средствами для ее достижения. Для того чтобы связать цель со средствами, необходимо учесть множество факторов, которые не всегда возможно выделить или получить их оценки. Поэтому решение принимается в условиях неполноты и неопределенности информации. То, что в усложняющемся мире проблема принятия решения становится проблемой коллективного принятия решения [3], тоже отражено с помощью этого метода. На рассмотренном примере показали, что решение, полученное с помощью метода анализа иерархии, может быть использовано для задач принятия решения девелоперами о том, каким образом работать на рынке вторичного жилья.
1. Antonov, AV System analysis. [Text] / AV Antonov. - Moscow: Vyssh.shk., 2006. - 453 p.
2. Volkov, VN Systems theory and methods of system analysis in the management and communication [Text] / VN Volkova [et al.]. - Moscow: Radio and communication, 1983. - 248 p.
3. Volkova, V.N. Teoriya sistem i sistemnyy analiz: uchebnik dlya vuzov [Tekst] / V.N. Volkova, A.A. Denisov. - Moskva: Yurayt, 2010. - 679 s.
4. Volkov, VN Denisov, AA Bases, and system control theory analysis / VN Volkov, AA Denisov. - St. Petersburg: SPbGTU, 1997. - 510 p.
5. Download, VV Basic theory of systems and system analysis [Text] / VV Kachala. - Moscow:. Hotline - Telecom, 2007. - 216 p.
6. Saaty, T. Decision making. Analytic Hierarchy Process. [Text] / T. Saaty. - Moscow: Radio and communication, 1993. - 320 p.
7. Taha, Hemdi A. Introduction to Operations Research, 7th Edition [Text]: Per. from English / H. A. Taha. - Moscow: "Williams", 2005. - 912 p.
8. Systems theory and systems analysis in management of organizations [Text]: Reference: Textbooks / ed. V.N.Volkovoy and A.A.Emelyanova. - Moscow: Finance and Statistics: INFRA-M, 2009. - 848 p.
9. Electronic resource http://realty.dmir.ru/ros/prices/ceny-na-kvartiry-v-ta
10. Property for sale. Electronic resource https://www.cian.ru/
11. Volkov, VN Systems theory and systems analysis: the textbook for high schools [Text] / VN Volkov, AA Denisov. - Moscow: Yurayt, 2010. - 679 p.














